火车类比：流体系统中的流动和压力波

在某些应用中，压力脉冲或流量脉冲会带来负面影响。例如，在喷墨印刷中，即使温和的压力脉冲也会降低送墨系统的效率和最大流量。在压力脉冲达到更高的系统中，还会使影响印刷质量的油墨起泡和缺墨等更严重问题的风险增加。较高压力脉冲也会对部件寿命和可靠性产生负面影响。

KNF设计了新的FP系列低脉冲泵；即便在更具挑战性的应用中，这种泵也能实现更平稳的流量输送，而消除上述问题。KNF 利用一种新的专有仿真工具，可以准确预测流体系统中的流量和压力变化，大大加快了这些FP泵的开发过程。

管道在流体系统中的作用

理解管道的行为对于确定流体系统对流动脉冲的反应至关重要，就像单头隔膜泵那样。本文阐述了在输送脉冲流体的管道的行为中，哪些物理效应发挥重要作用。这些效应是：

• 流体摩擦（阻力）

• 管道内液柱的惯性 

• 管壁形变带来的管容量变化 

虚拟实验可用来帮助人们以视觉形式呈现和理解每个效应的物理学原理。如图1所示，该实验讨论增塑聚氯乙烯(PVC-P)管的行为：管的长度\(l\)为1.5米，内径\(d\)为4毫米，壁厚为1毫米；该管的出口端连接到在大气压下盛水的容器。在管道入口端，放置活塞以向管道内提供脉冲流\(\tilde{Q}\)。同时通过单独的入口向管道提供稳定的流量 \(\overline{Q}\) 。视频1和视频2显示该实验的两个动画案例。

我们将在管道上游端（绿色折线表示的位置）观察管道对这种稳态和非稳态流动组合的反应。在该位置，测定稳态\((\overline{p})\)和非稳态压力\((\tilde{p})\)贡献的总和。在该位置测定的压力和注入流量之间的比率是管道的水力阻抗\(Z\)，该阻抗随活塞的冲程频率\(n\)而变化。

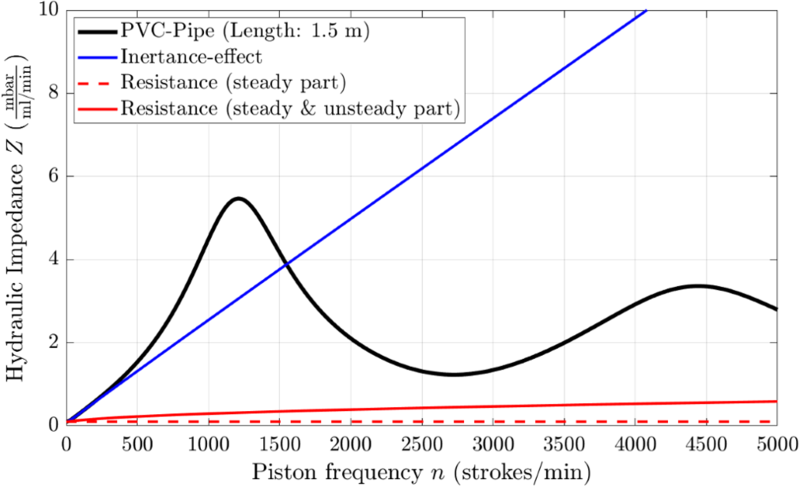
频率高达每分钟5,000次冲程时管道的整体阻抗响应在图2中显示为黑色实曲线。该阻抗响应将上面列出的所有三种效应（阻力、惯性、管壁形变）考虑在内，并代表管道的实际行为。下面将分别讨论每种物理效应。

流体摩擦

流体摩擦或管道阻力是首先研究的物理效应。这种效应是由管壁和管道中流动的液体之间的摩擦所引起的。这种效应通常考虑两种影响：稳态的（连续的）和非稳态的（脉冲）影响。描述稳态影响的物理定律早已众所周知的；可表达为，就连续流动的流体而言，只要流动状态是层流，管道中的压力损失\(\overline{p}\)就与管道中的流量\(\overline{Q}\)成比例(Hagen, 1839; Poiseuille, 1841)：

\(\begin{equation}\nonumber \bar{p} = \frac{128\eta l}{d^4\pi}\bar{Q} \end{equation}\)

其中\(\eta\)是管道中流体的动力粘度。因此，稳态流动的阻力是恒定的，不依赖于活塞频率，如图2所示（红色虚线）。此外，可以观察到，与实际测定的阻抗（黑色曲线）相比，稳态流动的阻抗很小。只有在零频率时，实际阻抗曲线（黑色曲线）才与管道的稳态阻力（红色虚线）相等。稳态和非稳态摩擦的总合在图2中显示为红色实线。非稳态阻抗不太为人所知；它呈频率依赖，与管道中的压力损失和流量非线性相关(Zielke, 1968)。如图2所示，就大多数活塞频率而言，与实际测定的增塑聚氯乙烯管道阻抗相比，组合阻力效应仍然很小。

为了有助于以视觉形式呈现这些流体阻力效应，我们用在直线轨道上行驶的快速列车来类比。先想象一下，火车匀速行驶——火车周围的空气产生摩擦力：这是火车发动机必须克服的稳态阻力。然后想象火车司机以小幅、谐波的方式周期性给火车加速和减速：这会造成额外的不稳定摩擦效应。

液体惯性

在本节中，仅考虑与管内液柱质量相关的影响。与质量相关的效应称为惯性。使用上面介绍的火车类比，这种效果可以轻松可视化。假设列车在直线轨道上以谐波振荡的方式来回运动。如果列车运行缓慢，则发动机提供的扭矩很小。但是，随着列车振荡速度提高，需要的扭矩越来越大。

类似地，如图1所示，在实验中积聚的压力也是如此。如果活塞的振动频率较低，则管道中积聚的压力较小。但是，如果振荡频率提高，则压力随施加的频率成比例提高。这种情况下产生的阻抗如图2中的蓝色实线所示。令人惊讶的是，惯性引起的阻抗（或压力脉冲）高于摩擦阻力效应。此外，可以观察到，当活塞运动频率较低时（不高于每分钟500个冲程），实际阻抗曲线和代表管道中惯性效应的曲线非常匹配。但是，当活塞运动频率更高时，差异变大，而且蓝色线性阻抗曲线不能再代表由黑色曲线表示的增塑聚氯乙烯管道的真实非线性阻抗。所以，一定有额外的效应导致聚合物管道的这种特殊行为。

管壁容纳

如图2中的黑色曲线表示的管道的典型非线性行为，只有在考虑管壁弹性的情况下才能得到解释。重要的事实是，管壁会有少量的膨胀和收缩；因此，根据管道中该位置的压力，一定量的流体会由于管壁的形变被储存或释放。这种效应称为容纳效应，源自我们可以想象管道包含沿管道走向均匀分布的小容器阵列。

同样，列车类比可以用来解释这种容纳效应；它表明容纳效应与惯性效应有很强的相互作用，如前一节所述。再想象一下，火车由直线轨道上的一辆机车和几节车厢组成。但是，这一次，在车厢之间不是使用刚性耦合，而是使用如弹簧或橡皮筋这样的柔性耦合。现在机车开始以振荡方式往复运动。低频时，车厢与机车同步（同相）移动，列车的行为类似于车厢之间的耦合是刚性的情况。如果列车的振荡频率提高，则车厢和耦合器开始相互作用，机车和车厢的运动变得异步。这种情况呈现于视频1；它代表图1中介绍的相同实验，但活塞频率为1,200冲程/分钟。

绿色的星表示在管道的开始、中间和末端流体粒子运动的振荡部分。如果观察第一颗星（火车头）和最后一颗星（列车的最后一节车厢），则可以看到粒子在这些位置的运动是异步的（异相）。在这种特殊情况下，第一个和最后一个流体粒子之间的相位差为90°。此外，沿管道的压力分布可用对应位置管壁的膨胀将其可视化。对于视频1中所选的活塞频率，可以观察到管道的运动作用在活塞上，因此1,200冲程/分钟时的阻抗值和压力脉冲（如视频1中的绿色曲线所示）非常高，远远大于仅阻力和惯性的组合效果。

如果活塞频率进一步提高，则当机车前后移动时，列车的最后一节车厢可能会“后前移动”（180°异相）。这种情况呈现于视频2，对应活塞频率为2,700冲程/分钟。观察第一颗星（火车头）和最后一颗星（列车的最后一节车厢）——您会看到粒子在这些位置的运动相位正好相差180°。同样，沿着管道的压力分布可视化为管壁的膨胀。在这种特殊情况下，管道似乎与活塞一起作用，因此2,700冲程/分钟时的阻抗值和绿色曲线中显示的管道入口处的压力脉冲显著降低（与1,200冲程/分钟时的结果相比）。

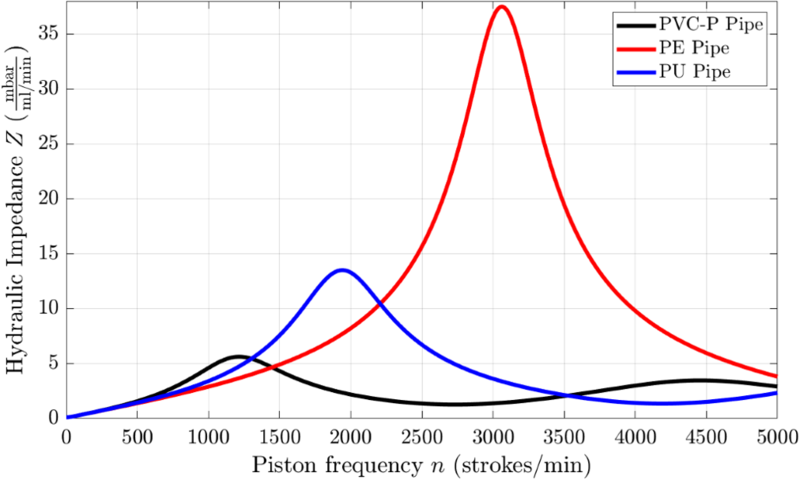
这两种特殊情况清楚地说明压力波和流动波是如何在管道中产生并与活塞相互作用的。这些波现象是阻抗曲线呈特殊形状的原因（如图2所示）。阻抗曲线的形状在很大程度上取决于管道的材料特性，如图3中的如下管道材料所示：聚乙烯(PE)、聚氨酯(PU)和增塑聚氯乙烯(PVC-P)。这些材料性能可通过KNF开发的特殊测定方法测得（Frey等人，2020）。

转换到真实的泵模拟

尽管上面的聚合物管道行为似乎很难捕捉，但这只是向包含隔膜泵的完整流体系统模拟迈出的一步。完整的系统描述必须考虑上游管道和泵之间的额外相互作用、下游管道和泵之间的相互作用以及整个泵的行为。这种模拟工具已经在KNF开发出来，并用于设计新泵；这将在KNF博客后续的一篇文章中介绍。此外，如果有详细的系统信息，则该模拟工具可用于分析客户系统中的KNF泵。但是，关于管道水力阻抗的知识已经显示出泵提供平稳流动的巨大潜力。对于零流量脉冲的连续流动，管道阻抗最小（见图2中的红色虚线），且与易于计算的管道阻力相同。对于非平稳流动，管道阻抗随频率而变化，仅考虑管道阻力来估计系统阻抗时的误差可能会很大，如图2中频率为1,200次冲程/分钟（示例）时的黑色曲线所示。

我们希望本技术博文有助于理解为什么在某些情况下波动现象会导致流体系统中的较大压力或流量脉冲。KNF的专家们深刻了解这些情况。如遇到问题，请毫不犹豫地联系相关销售中心，我们将尽力为您的情况找到解决方案。

参考文献

Frey, R., Güdel, M., Dual, J., & Staubli, T. (2020).具有储层-管道-振荡阀系统的小型粘弹性管道在频域方面基于相位和振幅的表征。液压研究期刊(Journal of Hydraulic Research)，58(3), 460-470. 

Hagen, G. (1839).Ueber die Bewegung des Wassers in engen zylindrischen Röhren [探析水在狭窄的圆柱形管道中的运动]。Annalen der Physik (46), 432–442. 

Poiseuille, J. L. (1841).Recherches expérimentales sur le mouvement des liquides dans les tubes de très-petits diamètres [小直径管道内液体运动实验研究 

diameters]。Comptes Rendus de l’Académie des sciences. 

Zielke, W. (1968).瞬态管道流动中的频率相关摩擦。基础工程期刊(Journal of Basic Engineering)，90 (1), 109–115.